LSTM 이론 파헤치기!!!
1. LSTM?
1-1. LSTM 이란?
LSTM은 어디서 어떻게 생겨난 아이디어일까?
아래의 바닐라 RNN을 한번 보도록 하자.

기본적인 RNN의 모양은 위와 같다. 아주 단순하게 전 Cell에서 넘어온 Hidden state 값과 이번 Cell의 input 값을 concat한 후 Non-linear activation 함수를 통해 다음 Cell에 전파시킬 값을 반환하는 형태다.

위의 공식과 같이 계산이 된다.
위와 같은 구조가 어떤 문제점이 있을까?

위 그림과 같이 RNN 셀이 여러개로 엮이게 된다면

맨 마지막 cell의 output값은 위와 같은 공식이 성립이 된다. 이 부분이 학습과정을 거치게 되면 역전파 과정을 거치며 tanh가 미분이 되게 되는데
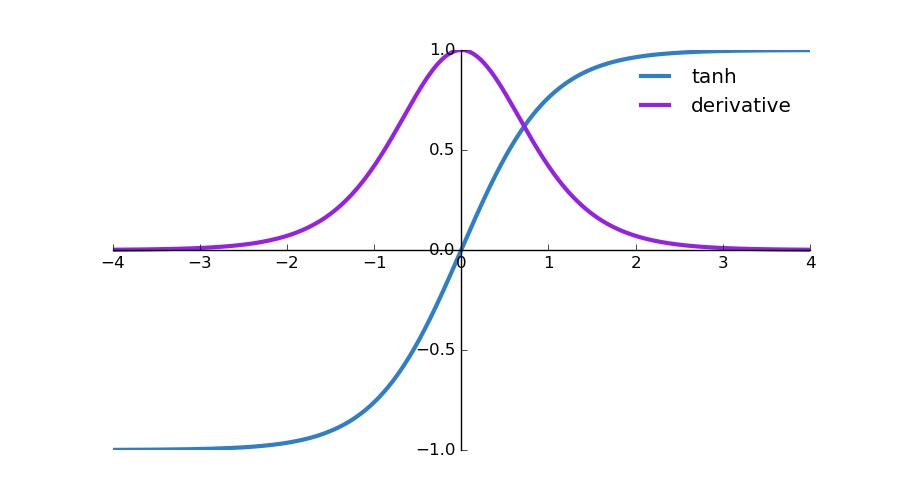
위 그림과 같이 tanh의 도함수는 0에서 1사이의 값이 된다. 0에서 1사이의 값을 계속 곱연산을 하게되면 점점 값이 0에 수렴하는 방향으로 가게된다. 그렇게 되면 위처럼 RNN 셀이 길게 늘어진 경우 초반의 입력이 후반으로 갈 수록 0이라는 값에 가까워지게 때문에 정보를 잃게된다. 이렇게되면 초반 입력이 후반 Cell에 영향을 거의 미치지 못하게 된다는 것을 알 수 있습니다. 이러한 현상을 Vanishing gradient problem이라고 부른다. 기울기 값이 사라지는 문제이다.
이러한 문제를 해결하기 위해 과거 Cell의 정보를 일정 필요한 만큼 기억해 나가자라는 개념에서 LSTM이 생겨났다.
그렇다면 LSTM은 어떻게 생겼을까?

위 그림과 같은 모양을 취하고 있다. 뭔가 복잡해 보이지만 제일 큰 변화는 Ct라는 과거 Cell state 정보를 따로 저장하는 변수가 생겼다는 점이다.
그렇다면 LSTM의 각 Gate들이 어떠한 역할을 해서 어떻게 output 값을 도출해내는지 알아보도록 하자.
처음으로 Forget gate를 볼 수 있다.

위 그림을 보면 ft를 구하기 위해 ht-1과 xt를 concat한 후 특정 가중치를 곱연산하여 sigmoid 함수를 통해 값을 도출했다. 이 ft는 현재 Cell의 입력들을 바탕으로 과거 Cell로부터 이어져온 정보들 중 어떤 정보를 얼마만큼 많이 남기고 어떤 정보를 얼마만큼 조금 남길것 인지를 정해주는 값이다.
Sigmoid 함수를 통과한 값은 0에서 1 사이의 값을 가지게 된다. 따라서 기존 정보에 sigmoid 함수를 통과한 값을 곱하면 그만큼 정보의 양이 줄어들게 되는 것이다.
예를 들어서 sigmoid를 통과한 값이 0.9다 라고 하면 해당 이전 정보를 0.9배 만큼 기억하게 되어 많이 기억하게 되고 sigmoid를 통과한 값이 0.1이라고 하면 해당 이전 정보의 0.1배 만큼만 기억하게 되어 조금 기억하게 되는 것이다.
이전 정보의 형태가 [0.1, 2.0, -0.4, 0.5] 이라고 하고 sigmoid를 통과한 값이 [0.1, 0.9, 0.4, 0.9] 라고 한다면 이전 정보를 [0.01, 1.98, -0.16, 0.45] 만큼만 남기고 나머지는 까먹자! 라고 해당 Cell에서 정하게 되는 것이다.
대신 정보를 까먹는 만큼 뒤에서 이번 셀에서 새로운 기억을 추가하는 과정이 있다.
Forget gate에서는 sigmoid가 0에서 1 사이의 값을 출력으로 하기 때문에 어떤 데이터를 얼만큼 더 혹은 덜 기억하게 하는 역할을 한다는 것을 알 수 있었다.
그 다음은 Input gate를 볼 수 있다.

forget gate에서는 과거의 Cell state 정보 중 어떤정보를 얼마만큼 까먹을까에 대한 내용이었다면 input gate는 이번 Cell에서의 입력 중 어떤 정보를 얼마만큼 과거 정보에 추가하여 더 기억해 나갈까를 정하는 부분이다.
그에 따라 위 그림에서 볼 수 있듯이 ~Ct에서는 vanilla RNN과 같이 tanh를 통해 현재 Cell의 정보를 구한다. 이후 it에서 그 정보를 얼마만큼 기억할지를 정하게 된다. 그러면 이번 Cell에서 어떤 내용을 얼마만큼 차후에 전파하고 싶을지가 정해지게 되는 것이다.
그 다음은 Cell state를 볼 수 있다.

위 그림에서 볼 수 있듯이 Ct-1에서 넘어온 과거 Cell들의 정보를 Forget gate를 통해 나온 값을 곱연산하여 특정 정보를 비율에 따라 잊고 Input gate를 통하여 이번 Cell의 input 데이터를 특정 정보 비율에 따라 앞으로 기억해 나갈 정보 값을 더해줘서 다음 Cell에 해당 정보를 전파하는 구조로 이루어져 있다.
마지막으로 Output gate 이다.

Output gate는 과거 Cell로부터 이어온 정보와 이번 Cell의 input data의 정보를 혼합하여 이번 Cell의 출력으로 내보내는 Gate이다.
이전 Cell로 부터 받아온 ht와 이번 Cell의 인풋인 xt를 sigmoid 연산을 하여 이번 Cell 인풋 데이터 중 어떤 정보를 얼만큼 남길지를 비율을 정하고 계산된 Ct에 tanh 연산을 통해 과거로부터 가져온 정보를 추출하고 두 정보를 곱연산을 통해 현재 정보로부터 과거로부터 이어온 정보를 얼만큼 남길지를 현재 Cell에서의 Output으로 정의한다.
이렇게 일련의 복잡한 과정을 통해 LSTM은 역전파 학습을 통해 각각의 gate의 W값이 변하면서 학습을 진행하게 된다.
어떻게 본다면 계산이 많이 복잡하고 변수도 많이 존재하기 때문에 비효율적이라고 판단될 수 있다. 그에 따라 GRU라는 알고리즘이 탄생하였다.
이 내용은 추 후 다루도록 하겠다.